【Python】NumPy,Pandas,Matplotlibと単回帰分析で家賃の予測値を求めてみる

ここまで、PythonのライブラリであるNumPy、Pandas、Matplotlibを扱って来ました。

これらの知識を使って、単回帰分析をやってみたいと思います。

ここでは関東のとある地域の高級マンションの広さと家賃のデータを使って家賃予測をやってみたいと思います。

単回帰分析をやると言っても、細かい統計的な知識、式の算出などをここでは扱いません。詳しい定義などは統計分析の書籍などで学んでください。ただ、分析自体は統計学で求められている結果の式などを利用するだけですので、難しく考える必要はありません。

単回帰分析で家賃の予測をやってみよう！

まず家賃のデータですが、rent.csvファイルとして用意していますので、こちらを利用していきます。この中には、x,yをラベルとしてそれぞれ部屋の広さ、家賃のデータが入っています。（もちろん適当なデータを自分で用意しても構いません）

ライブラリをインポートしてデータの読み込み

jupyter notebookを起動して、まずはライブラリのインポートをしまよう。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

そして先ほどのデータを読み込みます。データはダウンロードして、jupyter notebookで作業しているディレクトリと同じ場所に配置しておきます。

# データの読み込み
df = pd.read_csv('rent.csv')
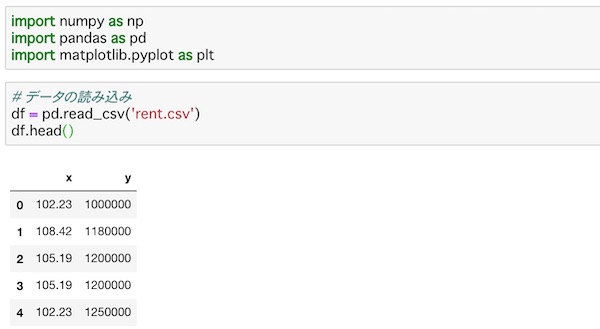
df.head()

read_csv()で先ほどのcsvファイルのデータを読み込んでいます。head()を使って冒頭の5つのデータを表示しています。

データをグラフに描画

このデータのxは広さ、yは家賃なのですが、これをグラフに描画してみます。

# xは部屋の広さ、yは家賃
x = df['x']
y = df['y']
plt.scatter(x, y)
plt.show()

データをそれぞれx,yにして、分布図を表示するscatter()を使ってshow()で表示します。

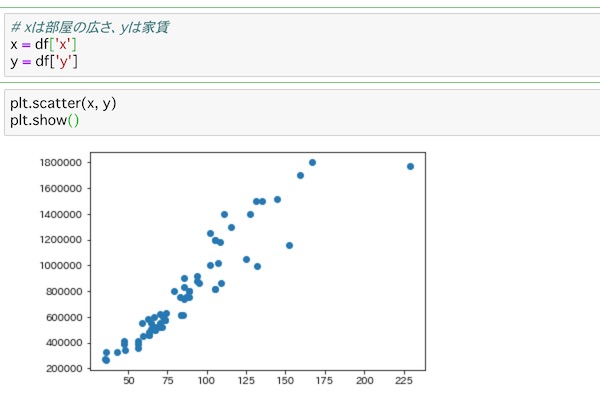
グラフを見ると、おおよそ右肩上がりの直線をイメージすることができます。

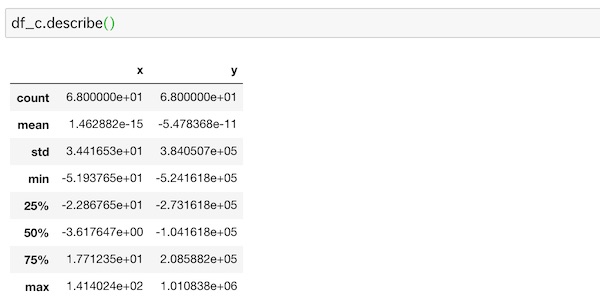
df.describe()

describe()を使ってデータの統計量を見てみます。

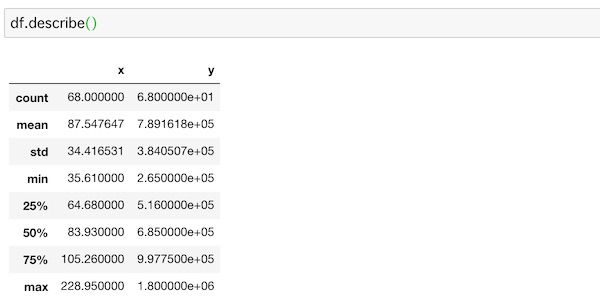
データ数や平均値などがわかります。

データの中心化

このデータを扱いやすいように中心化します。

データの中心化は、データからその平均を引く事で求めます。

#平均
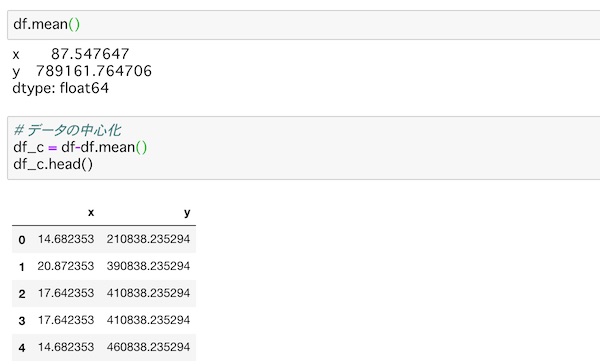
df.mean()
# データの中心化
df_c = df-df.mean()
df_c.head()

dfを使ってまとめて求めて、先頭のデータだけ表示しています。（df_cのcはセンタリングの意味でつけています）

センタリングしたデータの統計量はこうなります。

中心化したデータをグラフに描画

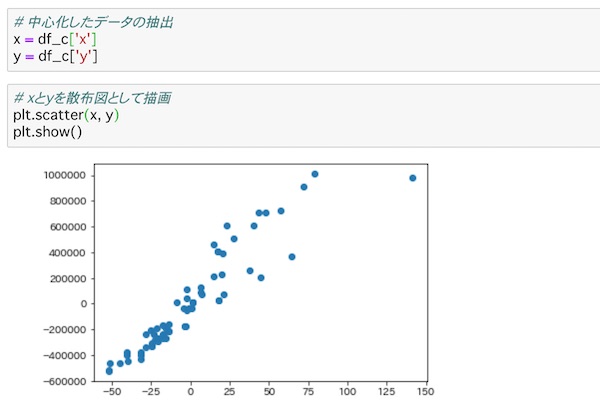
このセンタリングしたデータをグラフ化してみます。

# 中心化したデータの抽出
x = df_c['x']
y = df_c['y']
# xとyを散布図として描画
plt.scatter(x, y)
plt.show()

グラフ化は先ほどと同じ容量です。

単回帰を使ってグラフに描画

グラフの分布から右肩上がりの直線をイメージすることができます。ここから直線回帰を使うのが良いのだろうと考えることができます。いわゆるy = a*x + b の形ですね。

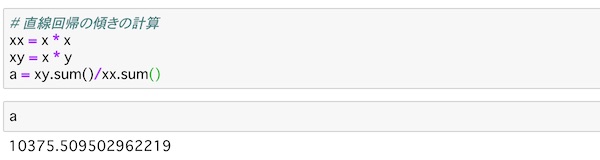
この単回帰には直線の傾きを求める必要があります。これは統計学的にはxの2乗の合計でxyの合計を割ったもので表すことができます。（ここの意味は統計の本などを参照してください）

# 直線回帰の傾きの計算
xx = x * x
xy = x * y
a = xy.sum()/xx.sum()

統計学の定義の通りに計算して直線の傾きaを求めています。

データを中心化した直線回帰の予測値を求める式はy=a*xで表すことができます。これをグラフに表します。

# 予測値　y=a*x　を描画
plt.scatter(x, y, label='実測家賃')
plt.plot(x, a*x, label='予測家賃', color='red')
plt.legend()
plt.show()

scatter()でx,yの分布を描画します。labelに「実測家賃」を指定します。plotで折れ線グラフが描画できるので、x, a*xのグラフを描きます。labelに「予測家賃」を指定し、見やすいように色を’red’に指定しています。legend()でlabelの凡例を表示するようにし、show()でグラフを描きます。

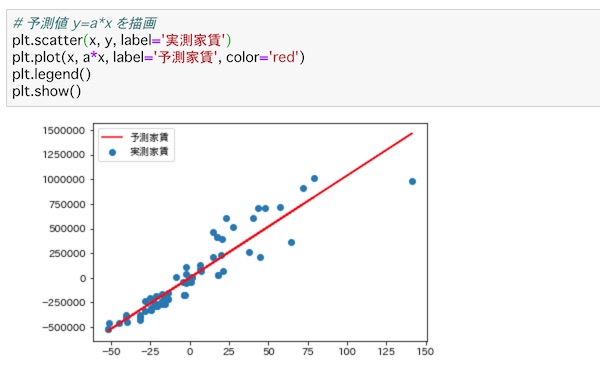
これで、実際の分布と予測値を見比べることができます。

予測値を求める関数を作る

これでグラフができましたが、予測式は中心化されたものですから、これを元に戻してそれぞれ値を与えて行けば、具体的な予測値を計算することができます。

関数を作る

それでも構わないのですが、手間でもあるので予測値を計算する関数を作ってみましょう。

# 予測式の直線の傾き
a
　# xの平均
df.mean()['x']
　# yの平均
df.mean()['y']

ここでは、傾きの値と、x,yのそれぞれの平均をあらかじめ求めておくことにします。

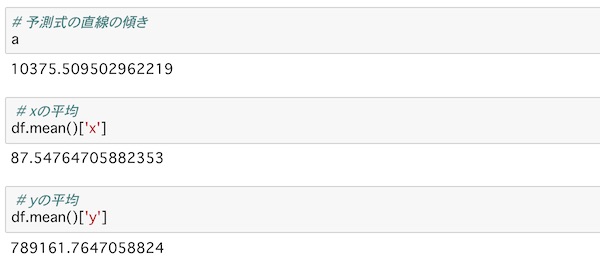
この値を使って関数を作ることにします。

# 予測値計算の関数の実装
def predict(x):
    # 定数
    a = 10375.509502962219
    xm = 87.54764705882353
    ym = 789161.7647058824
    # 中心化
    xc = x - xm
    # 予測値の計算
    y_hat = a*xc + ym
    return y_hat

aは傾き、xm、ymはx,yの平均です。これに先ほどの値を入れます。xcとしてxと平均値を使って中心化します。中心化した直線回帰の予測式はa*xでしたからa*xcにyの平均を加えることで、中心化から戻した値にすることができます。それをy_hatとして家賃の予測値を求めています。これを関数名perdict()として定義しています。

これで家賃の予測値を求める関数ができました。

予測値の計算

試しに、広さ95㎡の家賃の予測をしてみましょう。

# 広さ95㎡の家賃の予測値
predict(95)

perdict(95)で関数を呼び出します。

86万円超の家賃と予測できました。ちなみに使ったデータは六本木や青山の高級マンションのデータです。まあ、高いのは納得の値ですかね？

まとめ

PythonのライブラリであるNumPy、Pandas、Matplotlibを使って単回帰分析をやってみました。細かい統計的な知識、式の算出などは統計分析の書籍などで学ぶ必要がありますが、定義の結果だけを利用すれば、分析自体はできます。

もちろん、しっかりと統計学の知識を頭に入れて置くのも理解の助けにはなるはずです。